Note 概论信息论
..
Mean-squared-error 均方误差
cost = tf.reduce_sum(tf.pow(pred-Y, 2))/(2*n_samples)
可用于代价函数。线性问题中似乎比较受用。
均方误差 cost = E(pred - Y)^2 / 2, 1/2系数使得平方求梯度后常数系数为1,方便计算,系数对结果不影响。
Cross-entropy 交叉熵
cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred), reduction_indices=1))
度量两个概率分布间的差异性,可用于代价函数。逻辑分类问题似乎比较受用。
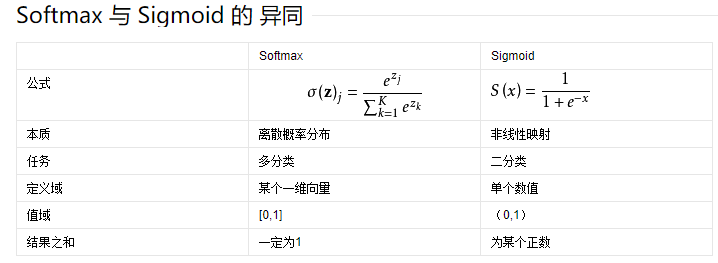
Softmax 归一化指数函数
将一个含任意实数的K维向量“压缩”到另一个K维实向量中,使得每一个元素的范围都在(0,1)之间,并且所有元素的和为1。 –百度百科
tf.nn.softmax(tf.matmul(x, W) + b)
可用于多分类问题的输出。在处理二分类时,可使用交叉熵作为损失函数。
Sigmoid 函数
同样将元素压缩到(0,1),但只对一个实数生效。可用于处理二分类问题。

扩展:激活函数的比较和优缺点